One major reason why fisheries scientists study fish growth, and describe it by means of the von Bertalanffy growth function (VBGF), is to perform stock assessments using the yield-per-recruit (Y/R) model of Beverton and Holt (1957), or one of its variants.
Thus, to optimize the use of the VBGF parameters, we have included a Y/R button to the POPGROWTH table which, when clicked on, leads to different forms of yield-per-recruit analyses being performed, depending on the entries in the table, and user’s choices. For definitions of some of the terms used below, see the section on POPGROWTH, ‘Natural Mortality’ and the LENGTH-WEIGHT tables.
However, before the available options are presented, the terms ‘recruit’ and ‘yield-per-recruit’ must be defined. Although the definition may vary between authors and between fisheries, we may here visualize recruits as fully metamorphosed young fish, whose growth is described adequately by the VBGF, and whose instantaneous rate of natural mortality is assumed similar to that of the adults. Such recruits have an average age tr, an average length Lr and an average weight Wr. Upon reaching age tr, the recruits may be caught immediately, in which case the mean age at first capture tc is equal to the age at recruitment (tc = tr). Alternatively, the recruits may be caught at a more advanced age (and correspondingly larger sizes, Lc and Wc). In such case, because of natural mortality, the number of recruits actually entering the fishery Rr will be less than the initial number of recruits Rc, or
![]()
![]() …1)
…1)
Thus, there is, for each combination of tc and F values, a yield-per-recruit (Y/R = catch in weight, per recruit), the value of which can be estimated from various equations whose exact form depends mainly on the model used to describe the growth of the fish. In the following paragraphs, equations for the estimation of Y/R are given for three forms of the VBGF, i.e.,
Case I: ![]() …2)
…2)
or standard VBGF (Beverton and Holt 1957), based on conversion from length using the isometric length-weight relationship
![]() …3)
…3)
where c.f. is the condition factor.
Case II: ![]() …4)
…4)
which is a form of the special VBGF (Pauly 1984) where the exponent (b) of the length-weight relationship is allowed to take values other than 3, i.e.,
![]() …5)
…5)
where b ¹ 3.
Case III: ![]() …6)
…6)
which is the VBGF for growth in length, and which can be used for relative yield-per-recruit analyses when a length-weight relationship is not available.
Estimation of yield-per-recruit
Case I is the original model of Beverton and Holt (1957), which has the form:
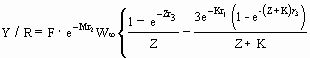
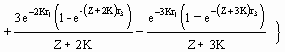 …7)
…7)
where Z = F + M ;
r1 = tc - t0 ;
r2 = tc - tr ;
r3 = tmax - tc ; and
where W¥ , K and t0 are growth parameters (see ‘POPGROWTH table’, this vol.), tc and tr are as defined above and tmax is "the maximum age of significant contribution to the fishery" (Ricker 1975) or more simply, the longevity, in open waters, of the fish in question (as given in the SPECIES table). The effect of the exact value of tmax is generally very small, and thus, when a suitably high value of tmax is not available, equation (7) can be considerably simplified by setting tmax = ¥ , in which case equation (7) becomes:
![]() …8)
…8)
whose parameters are defined as in Equation (7).
Both equations (7) and (8) can be used to assess the effect on yield-per-recruit of different values of tc, corresponding to different values of Lc, as generated, e.g., by different mesh sizes, and of F, corresponding to different levels of fishing effort.
The graphic routine included here allows viewing and printing two types of graphs: (a) plots of Y/R (always in g × year-1) vs. F (year-1), for values of Lc selected by the user (Fig. 29), or (b) complete ‘yield isopleth diagrams’, presenting yield-per-recruit contours for Lc/L¥ values ranging from 5 to 95% of L¥ , and values of F ranging from zero to an upper limit (default 5 year-1; max. = 20 year-1) set by the user (see Fig. 30, and Box 20).
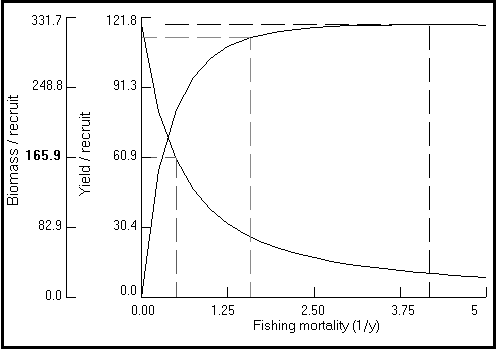
Fig. 29. Two-dimensional yield-per-recruit plot of Plectropomus leopardus. The parameters used are: W¥
=
2,220 g; K = 0.43 year-1; to = 0.34 year; M = 0.86 year-1; b = 3.2; tr = 0.12 year; and tmax = 26 years. Lc was
set to 20 cm. The descending curve shows the decrease in biomass/recruit as fishing mortality increases. The
ascending curve illustrates the small increase in yield when F is increased beyond F0.1 = 1.75 year-1. The units are g for biomass/recruit and g· year-1 for yield/recruit. Dotted lines indicate (from left to right): F value at which B/R is 50% of its original value (i.e., F0.5; F0.1); and Fmax, defined in Box 20.
In all these analyses, M is either taken from the POPGROWTH table (see section on ‘Natural Mortality’), entered by the user, or generated by the empirical equations of Pauly (1980), which, for length, takes the form
logM = -0.066 - 0.279logL¥ + 0.6543 logK + 0.4634 logT …9)
and for weight
logM = -0.2107 - 0.0824 logW¥ + 0.6757 logK + 0.4627 logT 10)
where M and K are expressed on an annual basis, L¥ and W¥ are expressed in cm (TL) and g (live weight), respectively, and where T is the mean environmental (water) temperature in ° C. [An internal routine converts low values of T (down to -2° C) to their higher physiologically effective equivalent (Pauly 1980); another routine converts values of L¥ originally expressed as SL or FL into TL, such that they can be used in equation (9); other measures of length (WD, OT or NA) are left unchanged.]
Fig. 30. Three-dimensional yield-per-recruit isopleth for Plectropomus leopardus as a function of
relative size at entry (Lc/L¥
) in the fishery, and of fishing mortality. The parameters used are: L¥
= 45
cm; M/K = 2; tc = 0.12 year; tmax = 26 years; and Lc = 20 cm. Note the small change in Lc/L¥
»
0.6 for maximum Y/R and fishing mortality > 1.5 year-1. See Box 20 for details.
The parameters W¥ and K are always taken from the POPGROWTH table, along with t0, when available, while an input routine allows entry of values of Lr and t0 higher than their default of zero (see Box 20); note that Lr must remain £ 50% of L¥ .
Case II
Equations (7) and (8) above assume that growth in weight is isometric (i.e. b = 3). This assumption is often not met in reality and the value of b in length-weight relationships generally ranges between 2.5 and 3.5 (see the LENGTH-WEIGHT table, this vol.). One method for dealing with values of b ¹ 3 is the use of the incomplete b -function, as proposed by Jones (1957); see also Ricker (1975).
Box 20. The yield-per-recruit and biomass-per-recruit graphs.
The Y/R routine included in FishBase is constructed such that Y/R and B/R plots are presented even if only L¥
and K are available in the POPGROWTH table, i.e., defaults are provided for the missing parameters, as follows:
Case I (see Yield-per-recruit Analyses, this vol.) is used when W¥
is available and b = 3. The initial plot assumes tr = 0, t0 = 0 (unless available in the POPGROWTH table), and Lc = 0.05 ×
L¥
, while M is treated as in Case III, except that it is equation (10) which is provided for the estimation of M. The parameters tr and t0 can be subsequently changed, the former via entry of a value of Lr (changed internally into tr), the latter by entry of a value of choice, or of a rough estimate, derived using an empirical equation of the form
log(-t0) »
-0.3922 - 0.2752 logL¥
- 1.038 logK
where L¥
is in cm (TL), and K in year-1, and which is based on 153 triplets of t0 , L¥
and K values selected from Pauly (1978) such as to cover a wide diversity of fish taxa and sizes (Pauly 1979). As equation (7) allows consideration of tmax, such value is taken from the SPECIES table when available; otherwise tmax = ¥
and equation (8) is used.
Case II is used when W¥
is available and b = 3; the treatment of t0, tr, Lc and M is as in Case I.
Case III is used when W¥
is missing and L¥
has to be used instead. This assumes b = 3, t0 = 0 , tmax = ¥
, tr = 0, and Lc = 0.05 ×
L¥
. Routines are provided for entry of values of M other than the default, set at M = 2K (an estimation routine is provided which uses equation (9), i.e., an input of T, in °
C, is required), and for varying Lc.
The B/R plots presented along with the Y/R analyses rely on modified versions of equations (7), (8), and (12), and should be considered when interpreting the Y/R plots (see below).
The plots themselves come in two forms: (1) 2D, with the shapes of the Y/R and B/R lines depending on Lc; and (2) 3D, i.e., as yield (or biomass) isopleth diagrams. The former plots show three reference points:
Emax or Fmax , i.e., the value of E or F associated with the highest Y/R value that is possible with a given value of Lc ;
E0.1 and F0.1, the value of E or F at which the slope of the Y/R is 1/10 of its value at the origin; and
E0.5 and F0.5 , the value of E or F associated with a 50% reduction of the biomass (per recruit) in the unexploited stock.
These reference points, corresponding to the three broken vertical lines in Fig. 29, are discussed in the concluding section of ‘Yield-per-recruit Analyses’.
References
Pauly, D. 1978. A preliminary compilation of fish length growth performance. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 55, 200 p.
Pauly, D. 1979. Gill size and temperature as governing factors in fish growth: a generalization of von Bertalanffy’s growth formula. Ber. Inst. Meereskd. Christian-Albrechts Univ. Kiel 63, 156 p.
Daniel Pauly
Here, yield-per-recruit, when tmax = ¥ , is given by
![]() …11)
…11)
where X = ![]() ;
;
P = Z/K ;
Q = b + 1 ;
b
= is the symbol of the incomplete beta function, while
r1 and r2 are defined as in equation (7).
The Y/R routine of FishBase automatically checks whether b = 3 or not. If not, equation (11) is used (see Box 20). The parameters used and the displays are otherwise the same as for equation (8).
Case III
When the parameters of a length-weight relationship are not available, Y/R analyses can still be performed, using the relative yield-per-recruit (Y’/R) concept of Beverton and Holt (1964) defined by
where c = Lc/L¥
, and the exploitation ratio is defined by E = F/Z.
Note that the relationship between Y/R and Y'
/R is given, other things being equal by
while the relationship between F and E is given by
Also note that the E scale is strongly non-linear, with E = 1 corresponding to F = ¥
. Hence, high values of E indicate effort levels that are always unsustainable, if not outright impossible to even achieve.
The use of the yield-per-recruit models: WARNINGS
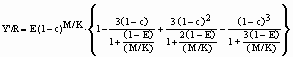 …12)
…12)![]() … 13)
… 13)![]() …14)
…14)
Yield-per-recruit models, although elegant and still suited to the management of certain stocks, should be used with caution. Fishers are not interested in an imaginary yield per recruit; they are interested in a physical yield of fish, and this is the product of the yield-per-recruit times the absolute number of recruits produced in the stock. Yield is directly proportional to yield-per-recruit over a wide range of fishing mortalities only if it can be assumed that there is no relationship—over a wide range of F or E values—between the size of the parental stock of fish and its progeny (which is not true, see the ‘RECRUITMENT table’, this vol.).
Thus, the values of F or E needed to produce a maximum yield-per-recruit will tend to generate very low yields, because Fmax and Emax usually reduce the parental stock to a level at which few recruits are produced. Moreover, it must be realized that the finding of yield-per-recruit analyses apply to long-term or equilibrium situations only. In the short term, an increase of fishing mortality or a decrease in size at first capture always results in higher yields, even when yield-per-recruit analyses predict lower yields. Similarly, a decrease in fishing mortality or an increase in size at first capture always results in lower yields in the short term, although, in the long run, higher yields may be reached. The duration of the transition period can be of several years in fish which have a high longevity and are subjected to exploitation over a number of years, as in a number of temperate stocks such as cod or halibut. In short-lived fish, the transition period will be much shorter; in the case of very short-lived fish, the distinction between short- and long-term effects does not even apply, because the stocks are never at equilibrium.
Another important feature of the yield-per-recruit approach is that yield-per-recruit is maximized at low values of F or E only in the case of large, long-lived, low mortality fishes. In small tropical fishes with high values of M, the values of F or E which maximize yield-per-recruit are generally high. Thus, managing a tropical fishery based only on Y/R analysis for a species of small fish (let alone a multi-species fishery) can be very misleading. [This account ignores the additional bias due to the assumption of knife-edge recruitment and selection implicit in equations (7), (8) and (12); see Pauly and Soriano 1986; Silvestre et al. 1991]
For this and related reasons, an (arbitrary) agreement has emerged to generally limit F to the point where the slope of the yield-per-recruit curve has 1/10 of its value at the origin of the curve (Gulland and Boerema 1973). This concept, called F0.1, may be viewed as a surrogate for MEY (Maximum Economic Yield), applicable in situations where economic data on the performance of a fishery are lacking. A concept analogous to F0.1, but applied to the exploitation ratio E is E0.1, is used in conjunction with Case III above.
Another safeguard when performing Y/R analysis is to always examine the corresponding biomass-per-recruit (B/R or B’/R) curve that is computed along with yield-per-recruit (one obtains B/R simply by dividing Y/R by F, see e.g., equation 8). Here, the appropriate reference point is the F (or E) value which reduces B/R (or B’/R) to half its unfished level (when F or E = 0), i.e., to the biomass level which¾ theoretically¾ maximizes surplus production and thus generates MSY (see Schaefer 1954, 1957; Gulland 1983; or Pauly 1984). This level is here referred to as F0.5 or E0.5 .
You get to Yield-per-recruit Analyses by clicking on the Biology button in the SPECIES window, the Population Dynamics button in the BIOLOGY window, the Growth button in the POPULATION DYNAMICS window and after selecting a study, the Y/R button of the GROWTH table. Alternatively, you can go to REPORTS, GRAPHS, POPULATION DYNAMICS, Y/R ANALYSES.
On the Internet, a relative yield-per-recruit analyses as well as an estimation of exploitation rate from length at first capture and average length is available if you click on the Key Facts link in the ‘More information’ section of the ‘Species Summary’ page.
Beverton, R.J.H. and S.J. Holt. 1957. On the dynamics of exploited fish populations. Fish. Invest. Ser. II. Vol. 19, 533 p.
Beverton, R.J.H. and S.J. Holt. 1964. Table of yield functions for fishery management. FAO Fish. Tech. Pap. 38, 49 p.
Gulland, J.A. 1983. Fish stock assessment: a manual of basic methods. FAO/Wiley, New York.
Gulland, J.A. and L. Boerema. 1973. Scientific advice on catch levels. Fish. Bull. (US) 71:325-335.
Jones, R.E. 1957. A much simplified version of the fish yield equation. Doc. No. P. 21. Paper presented at the Lisbon joint meeting of International Commission Northwest Atlantic-Fisheries, International Council for the Exploration of the Sea, and Food and Agriculture Organization of the United Nations. 8 p. [Mimeo].
Pauly, D. 1980. On the interrelationships between natural mortality, growth parameters, and mean environmental temperature in 175 fish stocks. J. Cons. CIEM 39(2):175-192.
Pauly, D. 1984. Fish population dynamics in tropical waters: a manual for use with programmable calculators. ICLARM Stud. Rev. 8, 325 p.
Pauly, D. and M. Soriano. 1986. Some practical extensions to Beverton and Holt’s relative yield-per-recruit model, p. 491-495. In J.L. Maclean, L.B. Dizon and L.V. Hosillos (eds.) The First Asian Fisheries Forum. Asian Fisheries Society, Manila.
Ricker, W.E. 1975. Computation and interpretation of biological statistics of fish populations. Bull. Fish. Res. Board Can. 191, 382 p.
Schaefer, M.B. 1954. Some aspects of the dynamics of populations important to the management of the commercial marine fisheries. Inter-Am. Trop. Tuna Comm., Bull. 1(2):27-56.
Schaefer, M.B. 1957. A study of the dynamics of the fishery for yellowfin tuna in the eastern tropical Pacific Ocean. Inter-Am. Trop. Tuna Comm., Bull. 2:247-268.
Silvestre, G., M. Soriano and D. Pauly. 1991. Sigmoid selection and the Beverton and Holt equation. Asian Fish. Sci. 4(1):85-98.
Daniel Pauly and Felimon C. Gayanilo, Jr.